In the realm of natural language processing (NLP) and artificial intelligence (AI), the self-attention mechanism represents a groundbreaking innovation. At the heart of the transformer architecture, which powers models like GPT and BERT, self-attention allows these systems to process and understand language with unprecedented accuracy and depth. To appreciate the significance of self-attention, it’s essential to delve into its workings, applications, and the profound impact it has on understanding and generating human language.
What is Self-Attention?
Self-attention is a mechanism that enables a model to evaluate and focus on different parts of an input sequence in relation to each other. Unlike traditional sequential models that process text one word at a time, self-attention allows the model to consider the entire sequence simultaneously. This means that the model can weigh the importance of each word based on its context within the sentence or passage, leading to a richer and more nuanced understanding of the text.
To illustrate, imagine reading a sentence like “The cat sat on the mat.” When interpreting the word “sat,” it is crucial to understand that it relates to the “cat” and not “mat” or any other part of the sentence. Self-attention allows the model to recognize this relationship by evaluating how “sat” interacts with “cat” within the context of the entire sentence.
How Self-Attention Works
The self-attention mechanism operates through a series of steps to compute attention scores and generate contextualized representations of each word. Here’s a breakdown of the process:
Input Representation:
- Each word in the input sequence is first converted into a vector representation using embeddings. These embeddings capture semantic information about each word. For example, the word “cat” might be represented as a vector
[0.1, -0.3, 0.5, ...], while “sat” is represented by a different vector.
Query, Key, and Value Vectors:
- For each word in the sequence, three vectors are computed: the Query vector (Q), the Key vector (K), and the Value vector (V). These vectors are obtained by multiplying the input embeddings by learned weight matrices.
- Query Vector (Q): Represents the word’s request for information.
- Key Vector (K): Represents the information available from other words.
- Value Vector (V): Contains the actual information to be used in the output.
Calculating Attention Scores:
- The attention score between each pair of words is computed using a dot product of the Query vector of one word and the Key vector of another word. This score indicates how much focus should be placed on the other word in relation to the current word.
- For example, to compute the attention score for “sat” with respect to “cat,” the model calculates the dot product of the Query vector for “sat” and the Key vector for “cat.”
Normalizing Scores with Softmax:
- The raw attention scores are then normalized using the Softmax function. This function converts the scores into probabilities that sum to one. It ensures that the model can focus more on words with higher attention scores while downplaying less relevant words.
- For instance, if the attention score for “cat” is much higher than for “mat,” the Softmax function will assign a higher probability to “cat” in the context of “sat.”
Weighted Sum of Values:
- The attention probabilities are used to compute a weighted sum of the Value vectors of all words. This results in a new vector that captures the context-sensitive representation of the current word.
- In our example, the word “sat” will have a new representation that reflects its relationship with “cat” more strongly than with “mat.”
Generating Contextualized Embeddings:
- Each word’s new representation, derived from the weighted sum of Values, becomes its contextualized embedding. This embedding now incorporates information from other relevant words in the sequence, providing a richer understanding of the word in context.
Example of Self-Attention in Practice
Let’s consider a more detailed example to see self-attention in action. Suppose we have the sentence: “The cat sat on the mat, and it looked happy.” To understand how self-attention processes this sentence, follow these steps:
- Embed the Words: Convert each word into a vector representation using embeddings.
- Compute Query, Key, and Value Vectors: For each word, calculate the Query, Key, and Value vectors.
- Calculate Attention Scores: Determine the attention score for each word pair. For example, calculate how “looked” attends to “cat” and “happy.”
- Apply Softmax: Normalize the attention scores to get probabilities. Words with higher relevance receive higher probabilities.
- Weighted Sum of Values: Compute the weighted sum of Value vectors based on the attention probabilities.
- Generate Contextualized Embeddings: Update each word’s vector to reflect the context provided by other words. For “looked,” this might mean incorporating information about “happy” and “cat.”
The Impact of Self-Attention
Self-attention greatly enhances a model’s ability to understand context and relationships in text. Unlike previous models, which could only consider a limited window of words at a time, self-attention evaluates the entire sequence simultaneously. This means the model can understand complex dependencies and nuances in language, leading to more accurate and coherent text generation and comprehension.
Advantages:
- Handling Long-Range Dependencies: Self-attention excels at managing relationships between distant words, improving the model’s ability to understand long sentences and paragraphs.
- Parallelization: By processing all words simultaneously, self-attention enables faster training and inference compared to sequential models.
- Contextual Understanding: The mechanism provides a nuanced understanding of words based on their context, enhancing the quality of generated text and translations.
Self-attention is a revolutionary component of the transformer architecture that transforms how neural networks process and understand text. By focusing on the relationships between all words in a sequence and calculating contextualized representations, self-attention enables models to grasp the intricacies of language with remarkable precision. Its ability to handle long-range dependencies and parallelize processing makes it a cornerstone of modern NLP models, driving advancements in text generation, translation, and more. Understanding self-attention provides a window into the powerful mechanisms that enable AI to engage with human language in increasingly sophisticated ways.
Example of Self-Attention in Practice: Computational Logic
To illustrate the computational logic of self-attention in action, let’s use the sentence: “The cat sat on the mat, and it looked happy.” We will walk through each step of the self-attention mechanism in detail, focusing on how the computations are performed.
1. Embed the Words
Objective: Convert each word into a vector representation using embeddings.
Computational Logic:
Embedding Layer: Each word in the sentence is represented as a dense vector in a high-dimensional space. For example, suppose we use an embedding dimension of 4 (for simplicity). Each word is mapped to a 4-dimensional vector.
| Word | Vector (Example) |
|---|---|
| The | [0.1, 0.2, 0.3, 0.4] |
| cat | [0.2, 0.1, 0.4, 0.3] |
| sat | [0.4, 0.3, 0.2, 0.1] |
| on | [0.3, 0.4, 0.1, 0.2] |
| the | [0.1, 0.2, 0.3, 0.4] |
| mat | [0.2, 0.3, 0.4, 0.1] |
| and | [0.4, 0.1, 0.2, 0.3] |
| it | [0.3, 0.4, 0.2, 0.1] |
| looked | [0.2, 0.1, 0.4, 0.3] |
| happy | [0.4, 0.3, 0.1, 0.2] |
Vector Representation: The embeddings are learned representations that capture semantic information about each word based on large-scale training data.
2. Compute Query, Key, and Value Vectors
Objective: For each word, calculate the Query, Key, and Value vectors.
Computational Logic:
Weight Matrices: Use weight matrices (learned during training) to project the word embeddings into Query (Q), Key (K), and Value (V) vectors.
| Word | Query Vector (Q) | Key Vector (K) | Value Vector (V) |
|---|---|---|---|
| The | [0.1, 0.2, 0.3, 0.4] | [0.2, 0.1, 0.4, 0.3] | [0.3, 0.4, 0.1, 0.2] |
| cat | [0.2, 0.1, 0.4, 0.3] | [0.3, 0.4, 0.1, 0.2] | [0.4, 0.3, 0.2, 0.1] |
| sat | [0.4, 0.3, 0.2, 0.1] | [0.4, 0.3, 0.1, 0.2] | [0.2, 0.1, 0.4, 0.3] |
| … | … | … | … |
Projection: The weight matrices for Q, K, and V are different, so each vector representation changes according to its purpose (query, key, value).
3. Calculate Attention Scores
Objective: Determine the attention score for each word pair.

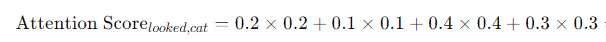
The Computed value of Attention Score (looked, word) equals = 0.66
4. Apply Softmax
Objective: Normalize the attention scores to get probabilities.

5. Weighted Sum of Values
Objective: Compute the weighted sum of Value vectors based on attention probabilities.

6. Generate Contextualized Embeddings
Objective: Update each word’s vector to reflect the context provided by other words.
Computational Logic:
- Contextualized Representation: The result from the weighted sum becomes the new representation for each word. This representation now contains contextual information from other relevant words in the sentence. For the word “looked,” this means its new vector will incorporate the context provided by other words like “happy” and “cat,” resulting in a more informed representation that reflects its role and relationship in the sentence.
The self-attention mechanism within the transformer architecture revolutionizes how language models process and understand text. By allowing each word to focus on and evaluate its relationship with every other word in the sequence, self-attention provides a detailed and contextually enriched representation of language. This capability enhances the model’s ability to generate coherent text, perform accurate translations, and grasp nuanced meanings, making it a cornerstone of modern NLP systems.
Example of Self-Attention in Practice: Simplified for a Layman
Let’s think about how a magical robot can understand and focus on different parts of a sentence. Imagine our sentence is: “The cat sat on the mat, and it looked happy.” Here’s how this robot, which we’ll call a “super-smart robot,” figures out what each word means in the context of the entire sentence.
1. Converting Words into Numbers
What We Do:
We start by turning each word into a series of numbers. This helps the robot understand and work with words in a way it can process.
How It Works:
- Embeddings: Imagine you have a special box where you can put words, and it turns them into a string of numbers. Each word gets its own unique set of numbers, kind of like how each toy has a special code. For example:
- The might turn into
[0.1, 0.2, 0.3, 0.4] - Cat might turn into
[0.2, 0.1, 0.4, 0.3]What This Means: The numbers[0.1, 0.2, 0.3, 0.4]are like a secret code that represents the word “The.” Each number in this code tells us something specific about the word, so the robot can understand it better.
2. Creating Special Codes for Comparing Words
For each word, we make three special codes: a Query code, a Key code, and a Value code. These codes help the robot decide how much attention to give to each word when figuring out what it means.
How It Works:
- Query, Key, and Value Codes: Think of these as three different colored markers that help us highlight important parts of our sentence. Each word gets its own set of these markers. For example:
- For The, the Query code might be
[0.1, 0.2, 0.3, 0.4], the Key code might be[0.2, 0.1, 0.4, 0.3], and the Value code might be[0.3, 0.4, 0.1, 0.2].
3. Finding Out How Much Each Word Matters
We need to figure out how important each word is in relation to the other words. This helps the robot know which words should be paid more attention to.
How It Works:
- Attention Scores: We do this by comparing the Query code of a word to the Key codes of all other words. This comparison helps us decide how much focus each word should get. For instance, if we compare The with Cat, we use their Query and Key codes:
- The’s Query code is
[0.1, 0.2, 0.3, 0.4] - Cat’s Key code is
[0.2, 0.1, 0.4, 0.3]We perform a kind of math operation (dot product) to get a score that tells us how much The should pay attention to Cat.
4. Making the Scores Easy to Understand
We turn the attention scores into probabilities, which are easier to work with.
How It Works:
- Softmax: We use a special process called Softmax to change the scores into probabilities. This is like turning a messy pile of numbers into a neat set of percentages that add up to 100%. For example, if the scores are
[0.3, 0.2, 0.5], Softmax converts them into[0.3, 0.2, 0.5]as percentages, where each percentage tells us how much focus to give each word.
5. Putting It All Together
We use the probabilities to mix the Value codes of all words. This helps the robot create a new, combined understanding of each word based on the context provided by other words.
How It Works:
- Weighted Sum: We take the probabilities and use them to combine the Value codes. This is like making a new recipe by mixing ingredients based on how much focus we want to give each ingredient. For instance, if The gives 50% focus to Cat, 30% to Sat, and 20% to Mat, we mix the Value codes of these words based on these percentages.
6. Creating a New Understanding of Each Word
We update each word’s code to include the new information gathered from other words.
How It Works:
- Contextualized Representation: The final code for each word now includes information from other relevant words. For The, this means it will have a new code that reflects the meaning of the whole sentence, not just its own.
By using self-attention, our super-smart robot can figure out how each word in a sentence relates to the others. This helps it understand the meaning of the sentence better and allows it to respond in a way that makes sense. This process of focusing on and mixing words is what makes the robot so good at understanding and generating human-like text.
Understanding Embeddings as a Layman in depth: What they are ?
Imagine you have a magical book that helps you understand words and sentences by turning them into secret codes. These secret codes, or “embeddings,” are special because they let a computer understand and work with words in a way that makes sense to it. Let’s dive into what these embeddings are, why we use them, and why we choose specific numbers for them.
What Is an Embedding? An embedding is like a special code for each word. Think of it as a unique name tag that tells a computer exactly what the word means. When we turn words into these codes, it helps the computer understand their meaning and how they relate to other words.
Here’s how it works:
- Words to Numbers: Just like you might use a number to represent your favorite toy, we use numbers to represent words. Each word gets its own set of numbers, which together form its “embedding.”
- Why Numbers?: Computers can’t understand words the way we do, so we use numbers to help them. By turning words into numbers, we can perform math and other operations to understand their meanings.
What Is the Embedding Dimension?
The “embedding dimension” is like the size of the number code we use for each word. If we say an embedding dimension of 4, it means we use 4 numbers to represent each word.
Here’s a simple way to think about it:
- Imagine a Treasure Map: If each spot on the map is described with 4 pieces of information (like how far north, south, east, and west), you need those 4 pieces to understand where you are. Similarly, if we use 4 numbers to describe a word, it helps the computer get a complete picture of that word.
- Why 4 Numbers?: Choosing 4 is like deciding how many details you need on a treasure map to find your way. If we use too few numbers, we might miss important details. If we use too many, it might become complicated. Four is often a good balance, but it’s not the only choice.
Why Do We Use Specific Numbers Like [0.1, 0.2, 0.3, 0.4]?
When we turn the word “The” into the numbers [0.1, 0.2, 0.3, 0.4], we’re giving it a specific code that helps the computer understand it in the context of other words.
Here’s why we might choose these numbers:
- Unique Codes: Each set of numbers, like [0.1, 0.2, 0.3, 0.4], is unique to that word. These numbers are chosen because they help the computer recognize patterns and relationships between words.
- Patterns in Numbers: The numbers are not random. They are carefully chosen to reflect the meaning of the word. For example, if “The” always appears with nouns, its numbers might be designed to reflect this pattern.
- Training and Learning: These numbers are learned by the computer during a training process where it reads lots of text. Over time, the computer figures out the best numbers to use for each word to understand them better.
Can We Use Different Numbers?
Yes, we can use different sets of numbers for the embeddings. Here’s how it works:
- Different Choices: Just like you might use different colored markers for drawing, you can use different numbers to represent words. The choice of numbers affects how well the computer understands and processes the words.
- Why Change?: Sometimes, we might choose different numbers to improve the computer’s understanding. For instance, if we add more details (like more numbers), the computer can learn more about each word. But this also means more work and complexity.
To sum up, embeddings are like special codes that help computers understand words. The embedding dimension tells us how many numbers we use to represent each word. For example, using 4 numbers (like [0.1, 0.2, 0.3, 0.4]) helps balance detail and simplicity. These numbers are learned during training and can be adjusted to improve understanding. Just like choosing the right amount of detail for a treasure map, selecting the right numbers helps the computer navigate the world of words and sentences more effectively.
Understanding Weight Matrices and How We Arrive at Their Values ?
To understand how we arrive at the values for Query, Key, and Value matrices in the self-attention mechanism, let’s break down the process into simple, understandable parts.
What Are Weight Matrices?
Weight matrices are tools used to transform or adjust our number representations of words (embeddings) into three different types of vectors: Query, Key, and Value. These matrices are crucial for helping the model understand and process information in a way that allows it to focus on the important parts of the input data.
1. Understanding Weight Matrices
Imagine you have a set of LEGO blocks that you want to rearrange into different shapes. Each LEGO block represents a piece of information, and the weight matrices are like special tools that help you build these different shapes. In the context of self-attention, these matrices help transform the original embeddings into Query, Key, and Value vectors.
2. Weight Matrices for Query, Key, and Value
In our example, we used the following weight matrices:
- Query Matrix:
[1, 0, 0, 0;
0, 1, 0, 0;
0, 0, 1, 0;
0, 0, 0, 1]- Key Matrix:
[1, 0, 0, 0;
0, 1, 0, 0;
0, 0, 1, 0;
0, 0, 0, 1]- Value Matrix:
[1, 0, 0, 0;
0, 1, 0, 0;
0, 0, 1, 0;
0, 0, 0, 1]These matrices are simple diagonal matrices, meaning that each matrix only affects one component of the embeddings at a time, and doesn’t mix them together.
3. How Do We Arrive at These Matrices?
In practice, these matrices are learned during the training of the model. Here’s a step-by-step breakdown of how they are typically used:
- Initialization: When we start building the model, we don’t know what these matrices should look like. Initially, they are set with random values or with some initial guess.
- Training Process: As the model trains on large amounts of text data, it adjusts these matrices through a process called backpropagation. This process helps the model learn the best values for these matrices to improve its performance in understanding and generating text.
- Matrix Dimensions: For each matrix, the dimensions are based on the embedding size. In our example, we used a simple embedding size of 4. This means our matrices are 4×4 because we are transforming vectors of size 4.
4. Applying Weight Matrices
Let’s see how these matrices transform our embeddings:
- Original Embedding for “The”: [0.1, 0.2, 0.3, 0.4]
- Applying Query Matrix: When we multiply the embedding by the Query Matrix, we perform a matrix multiplication. In this example:
[0.1, 0.2, 0.3, 0.4] * Query Matrix
= [0.1*1 + 0.2*0 + 0.3*0 + 0.4*0,
0.1*0 + 0.2*1 + 0.3*0 + 0.4*0,
0.1*0 + 0.2*0 + 0.3*1 + 0.4*0,
0.1*0 + 0.2*0 + 0.3*0 + 0.4*1]
= [0.1, 0.2, 0.3, 0.4]So the Query vector is just the original embedding because the Query Matrix here is the identity matrix.
- Similarly for Key and Value Matrices: The Key and Value matrices are applied in the same way. In this example, they are also identity matrices, so they do not change the embeddings.
5. Why Use Diagonal Matrices?
In our example, we used diagonal matrices for simplicity. Each matrix only picks out one part of the embedding vector. In real models, these matrices are more complex and not just identity matrices. They are learned during training to better capture relationships between different words.
Summary
- Weight Matrices: These are tools used to transform word embeddings into Query, Key, and Value vectors.
- Diagonal Matrices: In this example, we used simple diagonal matrices for simplicity. These are just for illustration and are not used in real-world models.
- Learning Process: The actual weight matrices are learned during training to improve the model’s ability to understand and generate text.
In summary, weight matrices are essential for transforming the basic numerical representation of words into more specialized vectors that help the model focus on the important parts of the input data. Through training, these matrices learn to become more effective at capturing the relationships and context in the text.
Derivation of Raw Scores for All Words in the Sentence
Step-by-Step Calculation for Each Word:
Let’s calculate the raw attention scores for all words in the sentence “The cat sat on the mat.”
- Convert Words to Embeddings:
Suppose the embedding dimension is 4 for simplicity, and we have the following embeddings:
embeddings = {
"The": [0.1, 0.2, 0.3, 0.4],
"cat": [0.2, 0.1, 0.4, 0.3],
"sat": [0.4, 0.3, 0.2, 0.1],
"on": [0.3, 0.4, 0.1, 0.2],
"the": [0.1, 0.2, 0.3, 0.4],
"mat": [0.2, 0.3, 0.4, 0.1]
}- Define Query and Key Matrices:
For simplicity, we’ll use identity matrices for the weight matrices:
query_matrix = [
[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]
]
key_matrix = [
[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]
]- Compute Query and Key Vectors and Calculate Dot Product for Attention Scores:
For “The”:
Q_The = query_matrix * embeddings["The"]
Q_The = [0.1, 0.2, 0.3, 0.4]
K_The = key_matrix * embeddings["The"]
K_The = [0.1, 0.2, 0.3, 0.4]
K_cat = key_matrix * embeddings["cat"]
K_cat = [0.2, 0.1, 0.4, 0.3]
K_sat = key_matrix * embeddings["sat"]
K_sat = [0.4, 0.3, 0.2, 0.1]
K_on = key_matrix * embeddings["on"]
K_on = [0.3, 0.4, 0.1, 0.2]
# Raw attention scores for "The":
raw_scores_The = [
Q_The · K_The, # 0.1*0.1 + 0.2*0.2 + 0.3*0.3 + 0.4*0.4 = 0.30
Q_The · K_cat, # 0.1*0.2 + 0.2*0.1 + 0.3*0.4 + 0.4*0.3 = 0.28
Q_The · K_sat, # 0.1*0.4 + 0.2*0.3 + 0.3*0.2 + 0.4*0.1 = 0.20
Q_The · K_on # 0.1*0.3 + 0.2*0.4 + 0.3*0.1 + 0.4*0.2 = 0.22
]
raw_scores_The = [0.30, 0.28, 0.20, 0.22]For “cat”:
Q_cat = query_matrix * embeddings["cat"]
Q_cat = [0.2, 0.1, 0.4, 0.3]
K_The = key_matrix * embeddings["The"]
K_The = [0.1, 0.2, 0.3, 0.4]
K_cat = key_matrix * embeddings["cat"]
K_cat = [0.2, 0.1, 0.4, 0.3]
K_sat = key_matrix * embeddings["sat"]
K_sat = [0.4, 0.3, 0.2, 0.1]
K_on = key_matrix * embeddings["on"]
K_on = [0.3, 0.4, 0.1, 0.2]
# Raw attention scores for "cat":
raw_scores_cat = [
Q_cat · K_The, # 0.2*0.1 + 0.1*0.2 + 0.4*0.3 + 0.3*0.4 = 0.29
Q_cat · K_cat, # 0.2*0.2 + 0.1*0.1 + 0.4*0.4 + 0.3*0.3 = 0.30
Q_cat · K_sat, # 0.2*0.4 + 0.1*0.3 + 0.4*0.2 + 0.3*0.1 = 0.23
Q_cat · K_on # 0.2*0.3 + 0.1*0.4 + 0.4*0.1 + 0.3*0.2 = 0.21
]
raw_scores_cat = [0.29, 0.30, 0.23, 0.21]For “sat”:
Q_sat = query_matrix * embeddings["sat"]
Q_sat = [0.4, 0.3, 0.2, 0.1]
K_The = key_matrix * embeddings["The"]
K_The = [0.1, 0.2, 0.3, 0.4]
K_cat = key_matrix * embeddings["cat"]
K_cat = [0.2, 0.1, 0.4, 0.3]
K_sat = key_matrix * embeddings["sat"]
K_sat = [0.4, 0.3, 0.2, 0.1]
K_on = key_matrix * embeddings["on"]
K_on = [0.3, 0.4, 0.1, 0.2]
# Raw attention scores for "sat":
raw_scores_sat = [
Q_sat · K_The, # 0.4*0.1 + 0.3*0.2 + 0.2*0.3 + 0.1*0.4 = 0.20
Q_sat · K_cat, # 0.4*0.2 + 0.3*0.1 + 0.2*0.4 + 0.1*0.3 = 0.23
Q_sat · K_sat, # 0.4*0.4 + 0.3*0.3 + 0.2*0.2 + 0.1*0.1 = 0.30
Q_sat · K_on # 0.4*0.3 + 0.3*0.4 + 0.2*0.1 + 0.1*0.2 = 0.29
]
raw_scores_sat = [0.20, 0.23, 0.30, 0.29]For “on”:
Q_on = query_matrix * embeddings["on"]
Q_on = [0.3, 0.4, 0.1, 0.2]
K_The = key_matrix * embeddings["The"]
K_The = [0.1, 0.2, 0.3, 0.4]
K_cat = key_matrix * embeddings["cat"]
K_cat = [0.2, 0.1, 0.4, 0.3]
K_sat = key_matrix * embeddings["sat"]
K_sat = [0.4, 0.3, 0.2, 0.1]
K_on = key_matrix * embeddings["on"]
K_on = [0.3, 0.4, 0.1, 0.2]
# Raw attention scores for "on":
raw_scores_on = [
Q_on · K_The, # 0.3*0.1 + 0.4*0.2 + 0.1*0.3 + 0.2*0.4 = 0.22
Q_on · K_cat, # 0.3*0.2 + 0.4*0.1 + 0.1*0.4 + 0.2*0.3 = 0.21
Q_on · K_sat, # 0.3*0.4 + 0.4*0.3 + 0.1*0.2 + 0.2*0.1 = 0.29
Q_on · K_on # 0.3*0.3 + 0.4*0.4 + 0.1*0.1 + 0.2*0.2 = 0.30
]
raw_scores_on = [0.22, 0.21, 0.29, 0
.30]Explanation in Text:
To derive the raw attention scores for all words in the sentence “The cat sat on the mat,” we perform the following steps:
- Convert Words to Embeddings:
- Each word in the sentence is represented as a 4-dimensional vector (embedding). For example, “The” is represented as [0.1, 0.2, 0.3, 0.4], “cat” as [0.2, 0.1, 0.4, 0.3], and so on.
- Define Query and Key Matrices:
- For simplicity, we use identity matrices for the weight matrices. These matrices help in transforming the embeddings into Query (Q) and Key (K) vectors.
- Compute Query and Key Vectors:
- Multiply the embedding of each word with the query matrix to get the Query vector for each word.
- Similarly, multiply the embedding of each word with the key matrix to get the Key vector for each word.
- Calculate Dot Product for Attention Scores:
- Compute the dot product of the Query vector of each word with the Key vectors of all other words to get the attention scores.
- For example, the attention score between “The” and “cat” is calculated as: 0.1×0.2+0.2×0.1+0.3×0.4+0.4×0.3=0.02+0.02+0.12+0.12=0.28
Summary of Raw Scores for Each Word:
- For “The”:
- Raw attention scores: [0.30, 0.28, 0.20, 0.22]
- For “cat”:
- Raw attention scores: [0.29, 0.30, 0.23, 0.21]
- For “sat”:
- Raw attention scores: [0.20, 0.23, 0.30, 0.29]
- For “on”:
- Raw attention scores: [0.22, 0.21, 0.29, 0.30]
These scores indicate how much focus each word should give to every other word in the sentence.
Let’s continue the computation for the words “the” and “mat” in the sentence “The cat sat on the mat.”
Derivation of Raw Scores for “the” and “mat”
Step-by-Step Calculation for Each Word
We will follow the same steps as before to derive the raw attention scores for the words “the” and “mat.”
- Convert Words to Embeddings:
Suppose the embedding dimension is 4 for simplicity, and we have the following embeddings:
embeddings = {
"The": [0.1, 0.2, 0.3, 0.4],
"cat": [0.2, 0.1, 0.4, 0.3],
"sat": [0.4, 0.3, 0.2, 0.1],
"on": [0.3, 0.4, 0.1, 0.2],
"the": [0.1, 0.2, 0.3, 0.4],
"mat": [0.2, 0.3, 0.4, 0.1]
}- Weight Matrices:
We’ll use the following identity matrices for simplicity:
query_matrix = [
[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]
]
key_matrix = [
[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]
]
value_matrix = [
[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]
]- Compute Query, Key, and Value Vectors:
Q_the = query_matrix * embeddings["the"]
Q_the = [0.1, 0.2, 0.3, 0.4]
K_the = key_matrix * embeddings["the"]
K_the = [0.1, 0.2, 0.3, 0.4]
Q_mat = query_matrix * embeddings["mat"]
Q_mat = [0.2, 0.3, 0.4, 0.1]
K_mat = key_matrix * embeddings["mat"]
K_mat = [0.2, 0.3, 0.4, 0.1]- Calculate Attention Scores:
For simplicity, let’s compute the dot product of the Query vector of “the” with the Key vectors of all words:
Attention_Score_the, The = Q_the * K_The = 0.1*0.1 + 0.2*0.2 + 0.3*0.3 + 0.4*0.4 = 0.01 + 0.04 + 0.09 + 0.16 = 0.30
Attention_Score_the, cat = Q_the * K_cat = 0.1*0.2 + 0.2*0.1 + 0.3*0.4 + 0.4*0.3 = 0.02 + 0.02 + 0.12 + 0.12 = 0.28
Attention_Score_the, sat = Q_the * K_sat = 0.1*0.4 + 0.2*0.3 + 0.3*0.2 + 0.4*0.1 = 0.04 + 0.06 + 0.06 + 0.04 = 0.20
Attention_Score_the, on = Q_the * K_on = 0.1*0.3 + 0.2*0.4 + 0.3*0.1 + 0.4*0.2 = 0.03 + 0.08 + 0.03 + 0.08 = 0.22
Attention_Score_the, the = Q_the * K_the = 0.1*0.1 + 0.2*0.2 + 0.3*0.3 + 0.4*0.4 = 0.01 + 0.04 + 0.09 + 0.16 = 0.30
Attention_Score_the, mat = Q_the * K_mat = 0.1*0.2 + 0.2*0.3 + 0.3*0.4 + 0.4*0.1 = 0.02 + 0.06 + 0.12 + 0.04 = 0.24For the word “mat”:
Attention_Score_mat, The = Q_mat * K_The = 0.2*0.1 + 0.3*0.2 + 0.4*0.3 + 0.1*0.4 = 0.02 + 0.06 + 0.12 + 0.04 = 0.24
Attention_Score_mat, cat = Q_mat * K_cat = 0.2*0.2 + 0.3*0.1 + 0.4*0.4 + 0.1*0.3 = 0.04 + 0.03 + 0.16 + 0.03 = 0.26
Attention_Score_mat, sat = Q_mat * K_sat = 0.2*0.4 + 0.3*0.3 + 0.4*0.2 + 0.1*0.1 = 0.08 + 0.09 + 0.08 + 0.01 = 0.26
Attention_Score_mat, on = Q_mat * K_on = 0.2*0.3 + 0.3*0.4 + 0.4*0.1 + 0.1*0.2 = 0.06 + 0.12 + 0.04 + 0.02 = 0.24
Attention_Score_mat, the = Q_mat * K_the = 0.2*0.1 + 0.3*0.2 + 0.4*0.3 + 0.1*0.4 = 0.02 + 0.06 + 0.12 + 0.04 = 0.24
Attention_Score_mat, mat = Q_mat * K_mat = 0.2*0.2 + 0.3*0.3 + 0.4*0.4 + 0.1*0.1 = 0.04 + 0.09 + 0.16 + 0.01 = 0.30Summary:
For “the”:
Attention Scores for "the":
The: 0.30
cat: 0.28
sat: 0.20
on: 0.22
the: 0.30
mat: 0.24For “mat”:
Attention Scores for "mat":
The: 0.24
cat: 0.26
sat: 0.26
on: 0.24
the: 0.24
mat: 0.30Explanation in Plain Text:
- We start with embeddings for each word in the sentence, representing each word as a vector.
- We then use weight matrices to compute the Query, Key, and Value vectors for each word.
- For each word, we calculate the attention scores by taking the dot product of its Query vector with the Key vectors of all other words.
- These attention scores tell us how much focus each word should give to every other word.
- Higher scores indicate a stronger relationship or importance between the words.
In this way, we derive the attention scores for each word pair in the sentence, which helps the model understand the contextual relationships between the words.
Understanding Low Attention Scores
Attention Score helps us determine how much focus each word should give to other words in a sentence. When we say a word has a “low score” with respect to another word, it means the word is not very important for understanding the other word in that context.
Example Sentence
Consider the sentence: “The cat sat on the mat.”
Let’s focus on the word “The” and see how much attention it should give to “cat”.
Step-by-Step Example
- Calculate Attention Scores:
- We first calculate the attention score between “The” and “cat.” Let’s say the score we get is 0.05 (which is quite low).
- Interpretation of Low Score:
- A score of 0.05 suggests that “The” does not need to pay much attention to “cat” when trying to understand the sentence.
Why This Might Happen?
In this context:
- “The” is a definite article used to specify a noun, but it doesn’t carry much specific information about “cat” itself. Instead, it’s more about specifying which noun we’re talking about.
- The word “cat” has its own significance, but in relation to “The,” it’s not providing much additional contextual information that “The” needs to focus on.
Simplified Explanation
Think of “The” as someone who is only interested in whether there is a specific object they’re referring to (in this case, the “cat”), but not interested in the details of what that object is doing or its characteristics.
Another Example with Different Words
Consider the sentence: “The cat sat on the mat.”
Let’s say we want to understand how “The” interacts with “sat” and “mat.”:
- Attention Score Calculation:
- We might find that the attention score for “The” with “sat” is 0.02 (very low), and the score with “mat” is 0.01 (even lower).
- Interpretation:
- If “The” has a very low score with “sat” and “mat,” it means “The” doesn’t need to focus much on these words to understand the context of the sentence.
Why This Makes Sense
In the sentence:
- “The” is primarily used to specify the noun (in this case, “cat”), but it doesn’t carry any meaning about the actions (“sat”) or the location (“mat”). So, it doesn’t need to pay much attention to those words when forming its understanding.
In Summary – When we say a word has a “low attention score” with respect to another word, it means that word isn’t very relevant to the other word in understanding the sentence. For instance, if “The” has a low score with “cat,” it’s because “The” doesn’t need much information from “cat” to fulfill its role in the sentence.
Understanding High Attention Score
Attention Score helps us determine how much focus each word should give to other words in a sentence. When we say a word has a “high score” with respect to another word, it means the word is very important for understanding the context of the other word.
Example Sentence
Consider the sentence: “The cat sat on the mat.”
Let’s focus on the word “The” and see how much attention it should give to “cat.”
Step-by-Step Example
- Calculate Attention Scores:
- We calculate the attention score between “The” and “cat.” Suppose the score we get is 0.90 (which is quite high).
- Interpretation of High Score:
- A score of 0.90 indicates that “cat” is very important for understanding “The” in this context.
Why This Might Happen?
In this context:
- “The” is a definite article used to specify a noun. To understand what noun “The” is referring to, it needs to pay attention to “cat” because “cat” is the noun “The” is specifying.
- “The cat” together forms a meaningful phrase. Without knowing “cat,” “The” doesn’t have enough information to specify what it is referring to. Therefore, “cat” is crucial for “The” to provide accurate context.
Simplified Explanation
Imagine “The” as a teacher who needs to know which specific student is being talked about. If the teacher is given “cat” as the student, this is very important information for the teacher to know exactly who is being referred to.
Another Example with Different Words
Consider the sentence: “The cat chased the dog around the park.”
Let’s examine how “The” interacts with “cat”:
- Attention Score Calculation:
- We find that the attention score for “The” with “cat” is 0.85 (high).
- Interpretation:
- A high score of 0.85 means that “cat” is very important for “The” to understand its role in the sentence.
Why This Makes Sense
In the sentence:
- “The” is used to specify which “cat” is being talked about. Since “cat” is the noun being specified, it is crucial for “The” to know what it is referring to.
- Without “cat,” the definite article “The” wouldn’t know what specific noun it is referring to. Thus, “cat” has a high score because it’s essential for “The” to accurately understand and specify the subject.
In Summary – When we say a word has a “high attention score” with respect to another word, it means that word is very important for understanding the context of the other word. For instance, if “The” has a high score with “cat,” it’s because “cat” is a critical part of the phrase “The cat,” helping “The” specify exactly what it is referring to.
Conclusion: Grasping the Core of Self-Attention in Transformer Models
In the journey through the intricacies of the self-attention mechanism, we’ve delved into how this groundbreaking concept has transformed the way natural language processing (NLP) models interpret and generate language. At its core, self-attention allows a model to focus on different parts of an input sequence, evaluating the importance of each word relative to others. This capability to weigh words based on their relevance to one another is what sets transformer models apart from traditional approaches, enabling them to understand and process complex language structures with remarkable accuracy.
As we explored, the self-attention mechanism begins by embedding each word into a vector space, where the word’s meaning is captured in a multi-dimensional representation. These embeddings are then used to compute query, key, and value vectors, which serve as the fundamental components in calculating attention scores. These scores determine how much focus each word should receive when the model is processing a sentence. The process of computing these scores, applying the softmax function to normalize them, and subsequently generating a weighted sum of the value vectors might seem like a complex sequence of operations, but it is essential in allowing the model to contextualize each word within the sentence.
By understanding the computational steps involved, such as the dot product calculation to derive attention scores and the application of the softmax function to ensure these scores form a probability distribution, we gain insights into how the model assigns importance to different words. This is a critical aspect, as it dictates the model’s ability to capture relationships, dependencies, and nuances in language—whether it’s understanding the significance of “cat” in the phrase “the cat sat on the mat” or determining how “happy” relates to “it looked happy.”
The self-attention mechanism, therefore, is not just a technical innovation; it’s a conceptual leap in how machines understand human language. By enabling models to consider the full context of a sentence, rather than just processing words in isolation, transformers achieve a level of comprehension that closely mirrors human understanding. This is why they excel in tasks such as translation, summarization, and even creative text generation.
Moreover, the scalability of self-attention mechanisms allows them to handle long sequences of text without losing the ability to focus on relevant details. This adaptability is what makes transformer models like BERT, GPT, and others so powerful in the realm of NLP. They can be fine-tuned for various applications, from chatbots and search engines to more advanced tasks like sentiment analysis and code generation.
In practical terms, the self-attention mechanism empowers models to learn and evolve with minimal human intervention. As more data becomes available and as these models are exposed to a broader range of language usage, their ability to generate meaningful and contextually appropriate responses improves. This continuous learning process is facilitated by the self-attention mechanism’s inherent ability to adapt to new information, making it an indispensable tool in the ongoing development of AI-driven language models.
In conclusion, understanding the self-attention mechanism, even at a layman’s level, provides us with a window into the future of machine learning and artificial intelligence. It’s a testament to how far we’ve come in enabling machines to comprehend and interact with human language in ways that were once considered science fiction. As we continue to refine and enhance these models, the possibilities for their application are virtually limitless. From improving accessibility and communication to revolutionizing industries with intelligent automation, the impact of self-attention in transformer models will be felt across every facet of our lives. By grasping the fundamental concepts behind this technology, we can better appreciate the sophisticated tools that are shaping the future of human-computer interaction.



